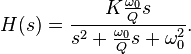Bygga ett bandpassfilter med hjälp av transformmetoder

[emilt]

Hallå! Jag läser just nu en kurs som heter "Transformmetoder". Vi har där fått en uppgift att med hjälp av Laplacetransformen bygga ett bandpassfilter som "släpper igenom" frekvensen 250Hz och dämpar de andra frekvenserna. Dämpningen för frekvenser under 240Hz och över 260Hz skall vara minst 3dB.

Enkelt tänkte jag, man behöver bara hitta överföringsfunktionen och "översätta" den till polär form för att då kunna hitta denna dämpning. Jag vet ju vad dämpningen skall vara för givna frekvenser så jag kommer få tre ekvationer med tre obekanta: L,C och R. Men det visade sig inte vara alltför enkelt...

Efter typ 6h vid denna uppgift har jag nu insett att mina elektronikkunskaper inte är på topp vilket antagligen sätter käppar i hjulet för mig. Är det någon som vet hur man går tillväga för att lösa en uppgift av detta slag? När jag väl hittat överföringsfunktionen G(s) så byter jag s mot jw. Jag har testat och detta ger exakt samma resultat som om man skulle använda jw-metoden från början. Jag vill sedan byta till polär form:

G(jw) --> K*e^(j@). För att hitta K antar jag att man tar realdelen av G(jw) i kvadrat plus imaginärdelen av G(jw) i kvadrat och sedan roten ur alltihop?

När jag då har ett uttryck för K så bestämmer jag L,R och C eftersom jag vet att K bör vara 1 då f=250Hz, samt att K bör vara 0,707... då f=240Hz eller f=260Hz. Jag antar att det är här jag gör fel för jag får då ut negativa värden på L, R eller C. Något tips?

I uppgiften står det också "Utgå från en konstruktion med en kondensator och en spole parallellt samt en resistor i serie med dessa". Detta tycker jag att man bara kan tolka på ett sätt och jag får då två fall enligt bilden nedan. Jag kan iaf inte komma på något annat fall som stämmer överens med detta. Oavsett vilket av fallen jag fokuserar på så får jag liknande problem, det är bara någon kvot som skiljer sig åt mellan fallen.



Hoppas någon förstår vad problemet är.

Tack på förhand!
/Emil

[Fransson]

Hej Emil.

På det här forumet tycker vi om när folk lär sig saker, och bidrar gärna till lärandet. Att lösa skoluppgifter är ett utmärkt sätt att lära sig saker. Därför brukar vi inte (inte jag i alla fall) lösa andras skoluppgifter. Det motverkar så att säga syftet.

Däremot kan jag ge några ledtrådar. Tänk efter nu. Vad känner du till om parallellresonanskretsar? Är deras impedans markant högre eller lägre vid resonansfrekvensen än vid andra frekvenser? Det borde hjälpa dig att välja koppling. Sen är det kanske inte alldeles nödvändigt att motståndet, bara för att det ska vara i serie, måste utgöra en spänningsdelare. Generatorkretsen och belastningen har även interna impedanser som påverkar filtret. För att söka tre okända värden brukar man behöva tre ekvationer.

Om läraren har sagt att ni ska använda ”Laplacetransformen” så borde lararen ha lärt ut det innan. Gå till baka till dina lektionsanteckningar och läs på eller ta fram läroboken och läs. Lösningen borde finnas där.

[emilt]

Hej Magnus! Tack för att du orkar läsa .

Syftet med tråden var självklart inte att få uppgiften löst åt mig utan snarare att få lite tips. Förhoppningsvis framgick det av inlägget men om inte så säger jag det nu iaf.

Tänk efter nu. Vad känner du till om parallellresonanskretsar?

Ja, det är väl här ett av problemen är. Jag kan inte speciellt mycket om parallellresonanskretsar, eller egentligen kan jag väl ingenting om dem. Har aldrig räknat på dem förr. Jag har dock för mig att impedansen är väl ganska rejält lägre just vid resonansfrekvensen?

Sen är det kanske inte alldeles nödvändigt att motståndet, bara för att det ska vara i serie, måste utgöra en spänningsdelare.

Här är jag nog lite borta, jag vet inte riktigt vad som menas med spänningsdelare. Menar du att jag i förslag 2 kan flytta R längst bort till höger? Problemet är väl då att jag inte kan ställa upp en diff.ekvation för u,ut(t) eftersom det inte går någon ström genom R och spänningen då skulle vara 0? Fast man kanske får anta att det ändå går en ström genom R i det fallet, trots att det inte är en sluen krets? Jag kanske är helt ute och cyklar...

När det gäller interna impedanser så är det ett idealt fall så vi har inga interna impedanser i spänningskällan.

Jag har ju fått ut en överföringsfunktion. Både genom att använda mig av impedanser och jw-metoden men också genom att ställa upp samband för spänningar (t.ex. spänning över spole är u = L*i'(t)). Oavsett om jag använder transformmetoder eller jw-metoden så får jag samma överföringsfunktion så jag antar att det är rätt så pass långt.

Men om jag ska ta ett exempel: Om vi tittar på förslag 1 så får jag följande samband:

U,ut = G(w) * U,in där G(w) är ett komplex funktion som beror av w (omega). Jag vill väl då uttrycka G(w) som i en polär form G(w) = K*e^(j@) där K då är beloppet av G(w)?

Se nedan hur mina resultat ser ut.


När jag då sätter in t.ex. att K = 1 för frekvensen 250Hz så leder det till att (wL)^2 = 0 vilket självklart måste vara fel. Jag antar då att jag gör något fel kanske när jag sätter att K = förstärkningsfaktorn?

Hälsningar
Emil Thalin

[Fransson]

Jag tycker det låter som om du har hoppat på en kurs som du inte har tillräckliga förkunskaper för.

Jag kan inte speciellt mycket om parallellresonanskretsar, eller egentligen kan jag väl ingenting om dem. Har aldrig räknat på dem förr.

Och impedansen är hög (med ideala ("resistansfria") komponenter oändlig) vid ressonans. Så du ska använda kopplingen enligt förslag 2 för att få ett bandpassfilter.

Och ω är en konstant som används för att omvandla "rotationshastighet" från radianer per sekund till varv per sekund. Då vinkeln "ett varv" är 2π radianer är ω=2π. Du kommer ofta stöta på 2π när något ska räknas i Hz ("varv" per sekund).

Edit:
Så det är mer riktigt att säga att G är en funktion av R,L och C, G(R,L,C)

[xxargs]

du saknar en generatorimpedans i serie i förslag 1
du saknar en lastimpedans i förslag 2

en spänningskälla är samma sak som kortsluten impedansmässigt och en strömgenerator är detsamma som öppen impedansmässigt


R2 i förslag 2 är till för att ge generatorn fix impedans (tex 50 Ohm) som nätverket arbetar emot - du måste också ha en lastimpedans på utgången (tex 50 Ohm) att mäta spänningen över och bör vara samma som generatorimpedansen (om du inte skall göra impedanstransform samtidigt) om du skall få några vettiga kurvor på simuleringen.

nätverket måste alltid beräknas mot ingång och utgångsimpedansen om det skall bli några vettiga resultat, det är inte som att räkna mot OP-ampar med nära oändlig impedans in och nära noll Ohm i impedans ut när man kör mot passiva grejor.

in och utimpedansen bestämmer en stor del av hela filtrets karaktär, utöver filterkopplingen i sig

[Fransson]

xxargs: Har du ens läst Emils inlägg? Eller tittade du bara på bilden innan du svarade?

Det är en beräkningsuppgift i skolan, inte någon simulering som krånglar.

Uppgiften från skola har jag tolkat som:
Generatorimpedans = 0Ω
Lastimpedans = oändlig.

[xxargs]

tydligen inte tillräckligt noga...

...ok det var ritsättet som lurade mig lite och tänkte fel väg och dubbelkollade inte

emilt: glöm mina kommentarer, beklagar detta

[emilt]

Jag tycker det låter som om du har hoppat på en kurs som du inte har tillräckliga förkunskaper för.

Grejen är att det är en mattekurs och inte en elektronikkurs. Dock så är just denna uppgift ett arbete som man då skall kunna lösa med hjälp av transformmetoder. Det som menas är då helt enkelt att man kan Laplacetransformera de olika derivatorna etc istället för att använda jw-metoden men jag tycker personligen att det kvittar vilken metod man använder, ingen är speciellt svår.

Problemet dyker som sagt upp när jag skall bestämma värden på L,R och C. Jag får ju fram en överföringsfunktion som då beror av L,R och C. Min idé är att skriva om den funktionen på formen K*e^(j@). Är det fel att göra denna omskrivning? När jag då gjort omskrivningen så antar jag att "konstanten" K är förstärkningsfaktorn för ett givet w. Dvs om w = 500pi så skall K = 1, och om w = 480pi så skall K = 0,707... Är detta antagande fel?

I förslag 2 får jag då fram följande samband:

Jag har här fått ut w0 genom att sätta in K=1 men detta är kanske fel?

När jag då sätter in mina värden på K och w så får jag 3 ekvationer med 3 obekanta men när jag sedan försöker lösa dessa får jag att R skall vara negativ och där tar det helt enkelt stopp...

[4kTRB]

Utan att ha läst igenom allt här så...
Enligt Wiki så har du den här formeln att utgå ifrån..

All band-pass second-order continuous-time have a transfer function given by

where

K is the gain (low-pass DC gain, or band-pass mid-band gain) (K is 1 for passive filters)
Q is the Q factor
ω0 is the center frequency
s = σ + jω is the complex frequency

Du får väl välja Q för önskad bandbredd antar jag.

[4kTRB]

Vidare så borde du kunna sätta H(s) = 1/sqrt(2) vilket är det amplituden
sjunkit till vid -3dB. Om du löser ut Q ur ekv. och anger en -3dB frekvens
så får du värden på Q som är lämpliga. Finns säkert forumister här som sysslar
med sånt här dagligen. Tänker du jobba som elektronikkonstruktör efter studierna?

[monstrum]

Om man gör lite snabbanalys av de två förslagen du ger så är förslag 1 uteslutet. Både DC och oändlig frekvens kommer att ge Uut = Uin, vilket inte ger någon dämpning. Skulle kunna tänka mig att man behöver spolar och kondensatorer med negativa induktanser och kapacitanser för att lösa det.

[4kTRB]

Använder du förslag 2 och tar fram överföringsfunktionen H(s)
för den kopplingen så får du exakt enligt Wikis och alltså ett
bandpassfilter. Där kan du identifiera de olika komponentvärden
och se vad Q motsvarar och vad w0 motsvarar.

Om du antar att insignalen är en sinusformad historia,
Ua = Acoswt
så kan du hoppas på att utsignalen också är sinusformad men antagligen fasförskjuten,
Ub = Bcos(wt+d)

Du vet att B ska vara minst -3dB utav A vid 2 olika frekvenser. Så det är det du kan titta
på för att få fram Q. Du skulle också kunna undersöka brytfrekvenser baserat på fasvinkeln
men då vill det så klart till att du vet vad den är vid -3dB.

[4kTRB]

Du kan nog inte hoppas på att få -3dB vid 240Hz och 260Hz då det hela troligen inte
kommer bli symmetriskt runt 250Hz. Men det var som sagt inget krav på.

Om insignalen är Acoswt så kan du skriva den transformerad som As/(s^2+w^2)
Applicerar du sedan den på H(s), alltså As/(s^2+w^2)*H(s) så får du ett uttryck
på utsignalen...

s^2(Aw0/Q)/ (s^4 + s^2(w^2+w0(1/Q+w0)) + s(w^2w0/Q) + (w0w)^2)

den kan du om du vill transformera till en tidsfunktion vilket kan vara en del bökigt
men såklart lärorikt om du nu går en mattekurs.

[4kTRB]

Betydligt enklare blir det om du skriver överföringsfunktionen H(s)= Ps/(s^2+Ps+Q) på
formen A/(s-s1) + B/(s-s2) och sedan inverstransformerar, så du får H(t) som då blir
på formen Ae^s1t + Be^s2t

Sedan multiplicerar du insignalen coswt med H(t) så får du utsignalen som funktion av tiden.
En sådan här uppgift med sinusformade signaler blir väldigt mycket enklare att beräkna med jw.
Då får du i så fall ersätta s med jw så slipper du transformera men det var väl det som uppgiften
gick ut på verkar det som.

[emilt]

Tänker du jobba som elektronikkonstruktör efter studierna?

Nej, det är väl inget jag har planerat. Jag tycker visserligen att elektronik kan vara intressant osv men då skulle det ev. vara på någon slags hobbynivå men jag har inte kommit igång med det intresset än. Har dock jobbat som elektronikmontör i ett par år så jag kan ju en del. Jag läser ett program som heter "Civilingenjörsprogrammet i Energisystem" så någon elektronik kommer jag antagligen inte hålla på med.

Jag ser att jag fått många tips men jag förstår dem inte helt och hållet. Jag vet ju att jag vill att förstärkningen skall vara 1/sqrt(2) vid frekvenserna 240Hz och 260Hz men betyder det att jag kan sätta att överföringsfunktionen H(s) som detta värde vid de frekvenserna? Måste jag inte skriva om funktionen på trigonometrisk form och sedan sätta det K som jag använt ovan som dessa värden?

Det vore trevligt att anta en insignal, transformera denna och sedan transformera tillbaks hela högerledet. Dock är det ingen metod vi får använda eftersom det skall vara godtycklig insignal.

Betydligt enklare blir det om du skriver överföringsfunktionen H(s)= Ps/(s^2+Ps+Q) på
formen A/(s-s1) + B/(s-s2) och sedan inverstransformerar, så du får H(t) som då blir
på formen Ae^s1t + Be^s2t
Sedan multiplicerar du insignalen coswt med H(t) så får du utsignalen som funktion av tiden.

Kan jag verkligen göra såhär? Om jag vet att U,ut(s) = H(s)*U,in(s) så är det inte ekvivalent med att u,ut(t) = h(t)*u,in(t).

När det gäller den formeln du hittat från Wikipedia:

All band-pass second-order continuous-time have a transfer function given by
Bild
where

K is the gain (low-pass DC gain, or band-pass mid-band gain) (K is 1 for passive filters)
Q is the Q factor
ω0 is the center frequency
s = σ + jω is the complex frequency

Så vet jag inte riktigt vad K och Q står för i detta fall. Jag kan tänka mig att du menar att Q = förstärkningsfaktor men K vet jag inte vad det är. Försökte söka på wikipedia om bandpassfilter men hittade inte det avsnittet som du länkat till.

Jag har ju fått fram att resonansfrekvensen w0 = 1 / sqrt(LC) men utöver det så är det stopp. När jag sätter K enligt min formel ovan som 1/sqrt(2) och sedan löser ut w så tänkte jag att jag borde få w1 och w2 som då motsvarar 240Hz samt 260Hz. Dock när man löser ut w så får man såklart två rötter varav den ena kommer vara negativ...

Tror ni det kan vara mening att denna uppgift inte skall gå att lösa analytiskt? Man kanske måste anta ett värde på C, typ 10nF och sedan se vad man får för bandbredd? Låter konstigt att det skulle vara så.