Bygga ett bandpassfilter med hjälp av transformmetoder

[4kTRB]

Det stämmer som du säger att det inte går att ta Uin(t)*H(t). Beräknar du H(t) så
får du impulssvaret. Det enda att göra är att omforma Uin till motsvarande Laplaceform
och multiplicera med H(s) och sedan inverstransformera resultatet.

Sedan så kan du nog inte få exakt -3dB-punkter vid 240Hz och 260Hz men däremot
minst -3dB som ju var kravet.

Räknar du på din kretsförslag 2 så får du att w0/Q = 1/RC. Passivt filter ger att K=1.

Det blir enklare att räkna med godtyckliga insignaler om du har H(s) på formen A/(s+s1) + B/(s+s2).
Fast det klart det blir en dell pyssel med att beräkna polerna s1 och s2 samt A och B.

Du kan ju alltid testa med lite olika Q i Wikiformeln. Sätt Q=6 => RC =6/w0

H(s) = s(w0/6) / (s^2 + s(w0/6) + w0^2) (skriv gärna om på formen A/(s+s1) + B/(s+s2))

multiplicera med s/(s^2+w^2) vilket motsvarar en insignal coswt och du har utsignalen som funktion av s.

[snigelen]

Edit2: Ok kimmen, jag borde ha sovit i stället. Det var både förvirrande och felaktig rappakalja .

[kimmen]

Börja med att räkna ut överföringsfunktionen för förslag 2. Det är ju bara en spänningsdelare där den "nedre" impedansen är parallellkopplingen av L och C.

Den blir slutligen på formen



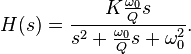
(lånar din bild där 4kTRB)

Ett av komponentvärdena kan du välja hur som helst eftersom du bara har två krav (bandbredd och resonansfrekvens) men tre obekanta. Tänk på att det inte kommer att vara möjligt att styra dämpningen vid 240 Hz och 260 Hz oberoende av varandra om du måste ha toppen vid 250 Hz.

[snigelen]

Dubbelpost

[snigelen]

Vad syftar du på där?

Den blir slutligen på formen

Slutligen? Man hamnar väl där mer eller mindre direkt? Även utan att blanda in Q (som inte fanns med från början, men väl kan vara en intressant storhet). Det grötiga börjar väl när man tar beloppet av överföringsfunktionen.

[kimmen]

Överföringsfunktionen är ju

Kod: Markera allt

        (1/RC) s
-----------------
(1/LC) + (1/RC) s + s^2

och om jag har räknat rätt stämmer beloppsuträkningen från tidigare


men det kan nog vara enklare att skriva överföringsfunktionen som

Kod: Markera allt

          1
----------------------
(R/L) (1/s) + 1 + RC s

vilket är samma som

Kod: Markera allt

          1
----------------------
1 + R( sC + 1/( sL ) ) 

och sedan räkna ut beloppskvadraten för s = jw som inte blir värre än

Kod: Markera allt

          1
-----------------------
1 + R^2(Cw - 1/(Lw))^2

Ur denna går det att se att beloppskvadraten (och därmed beloppet) visst blir 1 vid frekvensen där beloppet är som störst genom att titta på när (Cw - 1/(Lw))^2 är som minst, dvs 0 då Cw = 1/ (Lw) vilket är samma som w^2 = 1/LC. Då går det ju att välja L och C på något lämpligt sätt med detta villkoret uppfyllt.

Sedan kan man ju sätta beloppskvadraten till <= 0.5 vid gränsfrekvenserna. Detta leder till

1 <= R^2(Cw - 1/(Lw))^2 vid gränsfrekvenserna

som är ekvivalent med

|R| >= 1 / | Cw - 1/(Lw) | vid gränsfrekvenserna

och välj då R som det minsta positiva värde som uppfyller detta. Att byta tecken på R ger samma frekvenskurva men då för ett antikausalt system... Om R skall vara negativt eller positivt kommer alltså inte ut ur ekvationen för beloppet utan är något som man måste välja beroende på om det är ett kausalt eller antikausalt system. Och med tanke på att det skall vara en elektrisk krets så blir det det positiva.

[4kTRB]

Det vore trevligt att anta en insignal, transformera denna och sedan transformera tillbaks hela högerledet. Dock är det ingen metod vi får använda eftersom det skall vara godtycklig insignal.

Sätt s=jw så blir det enklast. Det du skriver ovan betyder väl inget annat än att du
måste ha H(s) och sedan multiplicera med godtycklig insignal?
Uppgiften går väl ut på att konstruera filtret först och främst?

Att man sedan vill kunna se resultatet med godtycklig insignal innbär ju i princip
att du måste ha med alla stationära delar likväl som de transienta delarna i ekvationen
för utsignalen.

[4kTRB]

Med en insignal coswt så kommer utsignalen troligtvis bli något i stil med

A*e^(s1*t) + B*e^(s2*t) + C*(s1*cos(w*t)+w*sin(w*t)) + D*(s2*cos(w*t)+w*sin(w*t))

där s1 och s2 polerna för H(s). Som syns är det 2 transienta delar och 2 stationära.

Men att utgå från den lösningen för att beräkna vad 1/RC ska vara för att få spärrbandsdämpningen
korrekt verkar vara rena mardrömmen eftersom termen 1/RC är inbakad i s1, s2, A, B,C och D.

[4kTRB]

Kunde naturligtvis inte låta bli att testa. Jag valde L och C för en centerfrekvens
på 1000rad/s och testade med R=50. R avgör hur snabbt insvängningsförloppet
sker. Lugnaste förloppet är det vid samma frekvens som centerfrekvensen w0.
Runt +/- 10rad verkar bandbredden hamna på i detta fallet.

[emilt]

Ok, bra att ni andra får samma överföringsfunktioner samt belopp som mig.

Men det stämmer alltså att denna uppgift inte går att lösa analytiskt?

Måste jag då testa med olika värden på C för att sedan bestämma L och R?

Jag har testat t.ex. med C = 10nF samt C = 1000nF vilket ger lite olika värden på L och R. När jag sedan kör en simulation i LTSpice så kan jag ju se förstärkningen som funktion av frekvensen. Jag får då t.ex. att vid 260Hz uppfylls kraven men vid 240Hz är förstärkningen för stor, typ -2,8dB. Samtidigt blir förstärkningen vid 250Hz ca -0,1dB vilket inte heller stämmer men rent praktiskt kanske detta inte går att åtgärda?

Jag antar att jag kan hitta något visst C värde som ger de resultat jag önskar genom att prova mig fram lite. Jag märkte t.ex. hur kurvan "förskjuts" åt höger när jag provade ett större C-värde så nog kan jag hitta något som passar. Men borde det inte gå att göra analytiskt?

[kimmen]

Ja nog går det att göra analytiskt, se mitt inlägg. Välj något L och C, vilka som helst, som ger toppen vid 250Hz och välj sedan R så att villkoren uppfylls vid båda gränserna.

Ett komponentvärde kommer du hursomhelst måsta ansätta till något. Detta kommer dock inte spela någon roll för överföringsfunktionen eftersom det enda som spelar roll är produkterna RC och LC. Ingångs- och utgångsimpedanserna beror dock på vilket värde du väljer.

t.ex. för
C = 10 µF vilket ger
L = 40.5 mH för toppen vid 250Hz

får jag

R >= 818.4 ohm för att uppfylla vid 260 Hz
R >= 772.6 ohm för att uppfylla vid 240 Hz

dvs R = 818.4 ohm för 1/sqrt(2) dämpning vid 260 Hz och en aning mer vid 240 Hz. (Eller för 10 nF, 40.5 H och 818.4 k-ohm.

Vill du ha exakt 1/sqrt(2) dämpning vid båda frekvenserna måste du förskjuta toppens frekvens en gnutta nedåt till det geometriska medelvärdet 249.80 Hz men det känns lite overkill att pilla med sånt.

[emilt]

Ok, det verkar som om jag fått det mesta att fungera nu. Visserligen blir min topp vid simuleringen kring 248Hz men det kanske kommer duga, får höra med läraren. Det kanske är omöjligt att få exakt så att förstärkningen blir 1 vid 250Hz samt att det skall vara minst -3dB vid 240Hz resp. 260Hz. Eller så har jag någon inställning fel i LTSpice.

Tackar alla för hjälpen iaf! Har varit mycket lärorikt .

[kimmen]

Prova att öka "Number of points per octave" i "AC Analysis"-rutan. För mig såg det fel ut först men då såg jag att min kurva var kantig.

[4kTRB]

Enligt Wikis formel så kan du identifiera w0/Q = 1/RC.

Q är önskad bandbredd i förhållande till centerfrekvens. 250/20 = 12.5 i ditt fall.

Då du redan valt L och C för din önskade centerfrekvens w0 så kan du beräkna R.

R = Q/w0/C = 12.5/500/pi/C

Ta tex C=100uF, L=4.053mH då ger ovanstående att R ska vara 80 ohm för att du ska
hamna väldigt nära dina uppsatta krav.

[emilt]

Ökade antalet points per decade från 100 till 1000 och nu hamnade min topp exakt på 250Hz samtidigt som de två gränsfrekvenserna uppfyllde de villkor jag ville. Toppen hade också en förstärkning på 0dB så nu är allt exakt som jag vill ha det!

För övrigt måste jag påpeka att detta program LTSpice verkar ju hur skoj som helst. Hur kan det vara gratis, måste ju tagit en evighet att programmera?

Tackar för hjälpen återigen!

Hälsningar
Emil