Svenska ElektronikForumet

Sitter med en PWM signal ut. Kan ställa frekvens och sedan är det 0-100% Duty som gäller.

Hur bör man designa och räkna ut för att få en relativt och jämn kurva ut? Det rör att styra en VFD från Mach3.

Ett normalt sätt verkar vara
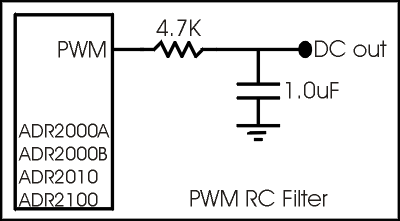
(Lånad bild)


Har provat lite men tycker signalen blir för jackig ändå. Kanske fel värden av mig?

Beror ju helt på vilken frekvens PWM signalen har.

edit, Här har du en kalkylator så du slipper räkna, bara ange frekvens och komponentvärden tills du har "relativt" jämn kurva, vad det nu är.
http://sim.okawa-denshi.jp/en/PWMtool.php

Min erfarenhet är att man inte får det helt hack-fritt med bara ett steg. Lägg ett likadant lågpassfilter till i serie med det, så bör det bli mycket bättre.

Testade för skojs skull lite snabbt med två steg med 100k ohm och 100nF och en 5V p-p fyrkant från funktionsgeneratorn. Vid 200Hz ligger utsignalen på 70mV p-p vid 50% duty, vid 1kHz är det nere på brus-nivå, med lite filtrering verkar det ligga på typ 5mV eller så.
Visst kan man räkna på det hela, men personligen så kan jag inte den matten och tycker dessutom att det går minst lika bra att bara testa sig fram.

Sen så bör man lägga en buffert direkt efter filtret också, krävs inte mycket innan det börjar svacka när man belastar samt mer brus lär komma i kablar och liknande när man driver det så högimpedivt..

Titta i denna tråden för lite tankar kring detta

http://elektronikforumet.com/forum/view ... =5&t=64448

Matematiken bakom behöver inte vara några konstigheter sålänge man känner till faltning.

• http://en.wikipedia.org/wiki/Convolution

Ett lågpassfilter av första ordningen har överföringsfunktionen

• \(H(s) \equiv \frac{1}{(1+\frac{s}{\omega_{0}})}\)

Genom invers Lapacetransform fås

• \(h(t) = \mathcal{L}\{{H(s)\}=\omega_{0} e^{-\omega_{0}t}\)

Med insignalen \(v_{in}(t)\) kan utsignalen beräknas genom faltning

• \(\displaystyle v_{ut}(t) = v_{in}(t)*h(t) = \int_{-\infty}^{\text{\ensuremath{\infty}}}v_{in}(t-u)h(u)\, du\)

Observera också att faltning mycket pedagogiskt kan uppskattas genom att rita upp signalerna som exempel från Wikipedia.


http://sv.wikipedia.org/wiki/Faltning

Klas-Kenny skrev:Visst kan man räkna på det hela, men personligen så kan jag inte den matten och tycker dessutom att det går minst lika bra att bara testa sig fram.

Det räcker med att kunna att filtrets gränsfrekvens ges av f_c = 1/(2*Pi*R*C) och sedan kan man mellan tumme och pekfinger säga att filtret släpper igenom signaler på 0 - 1/2 f_c helt opåverkade och vid 100 * f_c går 1% av signalens effekt igenom.

psynoise skrev:Observera också att faltning mycket pedagogiskt kan uppskattas genom att rita upp signalerna som exempel från Wikipedia.

Jo det är ju ganska pedagogiskt. Men det vore bra med ett kausalt exempel också/istället. Det blir ju ganska opedagogiskt som in/ut-signalexempel annars. I den bilden du har så stöter insignal och impulssvar på varandra vid tiden -1/2 och utsignalen börjar "därpå" vid tiden -1. Det hade varit bättre om både impulssvar och insignal började vid tiden 0, då hade även utsignalen gjort det.

4uf konding och 1k motstånd. Sedan körde jag på 1500hz i frekvens så funkar de fint att köra mot VFD´n